Factor x\left (3x5f\right) x (3x − 5f) View solution steps Solution Steps g ( x ) = 3 x ^ { 2 } 5 f ( x ) g ( x) = 3 x 2 − 5 f ( x) Factor out x Factor out x 1 What is (f−g)(x)?Set up the composite result function f (g(x)) f ( g ( x)) Evaluate f (g(x)) f ( g ( x)) by substituting in the value of g g into f f f ( x 9) = 9(x 9) f ( x 9) = 9 ( x 9) Cancel the common factor of 9 9 Tap for more steps Cancel the common factor f ( x 9) = 9 ( x 9) f ( x 9) = 9 ( x 9) Rewrite the expression
Www Humbleisd Net Cms Lib2 Tx Centricity Domain 3611 Answer review final exam fall Pdf
If f(x)=2^x-1+3 and g(x)=5x-9 what is (f-g)(x)
If f(x)=2^x-1+3 and g(x)=5x-9 what is (f-g)(x)-Then, f(x)g(x) = 4x 2 4x 1 = 1 Thus deg( f ⋅ g ) = 0 which is not greater than the degrees of f and g (which each had degree 1) Since the norm function is not defined for the zero element of the ring, we consider the degree of the polynomial f ( x ) = 0 to also be undefined so that it follows the rules of a norm in a Euclidean domainFind (fg)(x), (fg)(x), (f*g)(x) and (f/g)(x) for each f(x) and g(x) 2 f(x)= 8x^2 g(x)=1/x^2 I'm having trouble understanding what i have to do, please help This question is from textbook Algebra2 Answer by jim_thompson5910() (Show Source)



Http Www Hanbommoon Net Wp Content Uploads 13 08 Homework 9 Model Solution Pdf
G(x)= x2 1 x (8) f(x) = 3x 4 (9) f( ) = 3( ) 4 (10) f(g(x)) = 3(g(x)) 4 (11) f(x2 1 x) = 3(x2 1 x) 4 (12) f(x 2 1 x) = 3x 3 x 4 (13) Thus, (f g)(x) = f(g(x)) = 3x2 3 x 4 Let's try one more composition but this time with 3 functions It'll be exactly the same but with one extra step Find (f g h)(x) given f, g, and hFind the domain of the composite function f of gMathf(x)=x/math Function is giving the absolute value of mathx/math whether mathx/math is positive or negative See the y axis of graph which is mathf(x)/math against mathx/math, as x axis It shows y axis values or mathf(x
(f g)(2) = 10, (h – g)(2) = –9, (f × h)(2) = –12, (h / g)(2) = –05 If you work symbolically first, and plug in the x value only at the end, you'll still get the same results Either way will workLearn how to solve f(g(x)) by replacing the x found in the outside function f(x) by g(x) Using a linear approximation, estimate f(21), given that f(2) = 5 and f'(x) = square root 3x1 2 Educator answers eNotescom will help you with any book or any question
The composite function f g (x) is read as "f of g of x " The function g (x) is called an inner function and the function f (x) is called an outer function Hence, we can also read f g (x) as "the function g is the inner function of the outer function f "Find f(g(x)) f(x)=x^29 , g(x)=3x, Set up the composite result function Evaluate by substituting in the value of into Simplify each term Tap for more steps Rewrite as Expand using the FOIL Method Tap for more steps Apply the distributive property Apply the distributive propertyF(x)=x 2 2x−6 g(x)=x 4 3 3 jbouyer



Http Www Math Uakron Edu Norfolk H4221sol Pdf



Www3 Nd Edu Apilking Math Work Old exams Exam1f08soluutions Pdf
Explanation First, find g( −1) by substituting −1 for every occurrence of x in g(x) g(x) = x2 − 7x − 9 becomes g(−1) = (−1)2 −(7 ⋅ −1) − 9 g(−1) = 1 − ( − 7) − 9 g(−1) = 1 7 − 9 g(−1) = −1 Now, find f (g( − 1)) by substituting g( −1) or −1 for every occurrence of x in f (x) f (x) = x −2Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!SPM Add Math Form 4 FunctionThis short video is going to guide you how to find the f(x) using the substitution method Hope you find this method helpfu




F X X 2 What Is G X Brainly Com



Markwaltermath Weebly Com Uploads 2 2 1 9 Winter Break Part 2 Pdf
F(x)=x 4 −x 2 9 g(x)=x 3 3x 2 12 2 What is (f⋅g)(x)?Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutorCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music




Difrentiation Phpapp01




1 Evaluate The Following F X X2 1 And G X 3x 5 16 Points A S 3 B G 2 Homeworklib
Weekly Subscription $199 USD per week until cancelled Monthly Subscription $699 USD per month until cancelled Annual Subscription $2999 USD per year until cancelled 1 What is (f−g)(x)? In our example f takes the square of a number and adds 1 g doubles a number h subtracts 1 from a number So a verbal description of the composed f@g@h as a sequence of steps might be Subtract 1 Double Square Add 1 So in symbols we might describe this process thus x > x1 > 2(x1) > (2(x1))^2 > (2(x1))^21 So (f@g@h)(x) = f(g(h(x))) color(white)((f@g@h)(x)) = (2(x1))^21 color(white)((f@g@h)(x)) = 4(x^22x1)1 color(white)((f@g@h)(x)) = 4x^28x41 color(white)((f@g@h)(x)) = 4x^2



Secure Media Collegeboard Org Digitalservices Pdf Ap Apcentral Ap14 Calculus Ab Q3 Pdf




1 Let F X X2 1 And G X 3x A Evaluate Chegg Com
When you find (f o g)(x), there are two things that must be satisfied x must be in the domain of g, which means x is a real number (pretty easy to do) g(x) must be in the domain of f, which means that 1x 2 ^2 ≥ 4 (when you try to solve this, you get the empty set); B (1/4x)^2 will widen the parabola C 4x^2 is too wide to be g(x) D (16x)^2 is too narrow to be g(x) A is the correct answer When graphed on desmos com / calculator it shows this is the correct answer I hope this helped!\displaystyle{x}\in\mathbb{R},{x}\ne{1},{2} Explanation \displaystyle{f{{\left({x}\right)}}}\ \text{ is defined for all values of x except values which



Consider The Functions F X 2x 1 And G X X 2 10 What Is




Math Journal 9 11 Find The Value Of The Function Ppt Video Online Download
Domain of f(x) = x/(x^21) Extended Keyboard;F(input) = 2(input)3 g(input) = (input) 2 Let's start (g º f)(x) = g(f(x)) First we apply f, then apply g to that result (g º f)(x) = (2x3) 2 What if we reverse the order of f and g?Completing the square, f(x)=\frac{3}{4}(\frac{1}{x}\frac{1}{2})^2, so x=2 is a global minimum, and there is no minimum, absolute or relative, for x\gt 1 Completing the square, f ( x ) = 4 3 ( x 1 2 1 ) 2 , so x = − 2 is a global minimum, and there is no minimum, absolute or relative, for x > − 1




F X X2 What Is G X Um G X 2 1 Ob 9x O A 9 960 G3 O C G X 4x O D 9 X Brainly Com



Www Southhadleyschools Org Cms Lib Ma Centricity Domain 11 Theorems Pdf
When you combine the two domains to see what they have in common, you find the intersection of everything and nothing isGraph f (x)= (x1)^29 f (x) = (x − 1)2 − 9 f ( x) = ( x 1) 2 9 Find the properties of the given parabola Tap for more steps Use the vertex form, y = a ( x − h) 2 k y = a ( x h) 2 k, to determine the values of a a, h h, and k k a = 1 a = 1 h = 1 h = 1 k = − 9 k = 9 Since the value of a a is positive, the parabolaYou can put this solution on YOUR website!




F X X 2 What Is G X Brainly Com



Www Manhassetschools Org Site Handlers Filedownload Ashx Moduleinstanceid 4085 Dataid Filename Aimm 27 with key Pdf
You can put this solution on YOUR website!F(x)=x^4−x^29 g(x)=x^33x^212 (f−g)(x)= 2 What is (f⋅g)(x)? From the given graph it is clear that the vertex of f(x) and g(x) are same, ie,(0,0) But the graph of g(x) compressed vertically If k>1, then graph of g(x) stretched vertically and if k



Madasmaths Com Archive Maths Booklets Standard Topics Various Function Exam Questions Pdf



Www Frankstonisd Net Userfiles 70 Classes 343 1 2 6 7 inverse of a function Pdf Id 962
The slope of a line like 2x is 2, or 3x is 3 etc;4x 2x x x 2 4/7 2/7x 14x 4/7 3 7 9x 15 12x 4 24x 38x x Norman bought 116 feet of fencing to put around his backyard The backyard is a perfect squareWhen we reverse the order the result is rarely the same



Solution A Sketch The Graphs Of F X 9 X 2 And G X 3 X B Use The Laws Of Exponents To Explain The Relationships Between These Graphs Thank You




Com Converted Flip Ebook Pages 1 3 Anyflip Anyflip
Answer to If f(x) = x^2 and g(x) = x 1, what is f(g(x))?The Derivative tells us the slope of a function at any point There are rules we can follow to find many derivatives For example The slope of a constant value (like 3) is always 0;R where g(x)=x3 The function g has the set R for its range This equals the target of g, so g is onto



Www Boone Kyschools Us Userfiles 531 Classes 9731 Symbolic differentiation answer key Pdf Id




If F X X 2 What Is G X A G X 1 9x 2 B G X 1 3x 2 C G X 3x 2 D G X 1 3x 2 Brainly Com
G(x) → "g of x" → "operation(s), g, applied to a given quantity or value , x" "g(x) = x1" tells you to simply subtract 1 from whatever xvalue is given g(5)= 5–1=4 g(6)= 6–1=5 g(9)= 9–1=8 g(x)=x1 f(x) → "f of x" → "operations, f, applied to a g We substitute g(x) = x2 2x − 8 on the right side but we write (f (x)) everywhere that there is an x (gof)(x) = (f (x))2 2(f (x)) − 8 Substitute x − 1 for f (x) (gof)(x) = (x − 1)2 2(x − 1) − 8 Expand the square (gof)(x) = x2 − 2x 1 2(x −1) − 8 Use the distributive property (gof)(x) = x2 − 2x 1 2x −2 −8In this video we learn about function composition Composite functions are combinations of more than one function In this video we learn about f(g(x)) and g



Http Www Unit5 Org Cms Lib03 Il Centricity Domain 2651 Semester 2 final review solutions Pdf




Sketch The Graphs Of The Function F And G F X 9 X2 G X 2x 3 Study Com
Domain of f(x) = x/(x^21) Natural Language;Let f(x) = 9x^2, g(x) = 3x Find (fg) (x) f(x) = 9x^2 (1) g(x) = 3x (2) (1) and (2) being polynomials in x(f º g)(x) = f(g(x)) First we apply g, then apply f to that result (f º g)(x) = 2x 2 3 We get a different result!
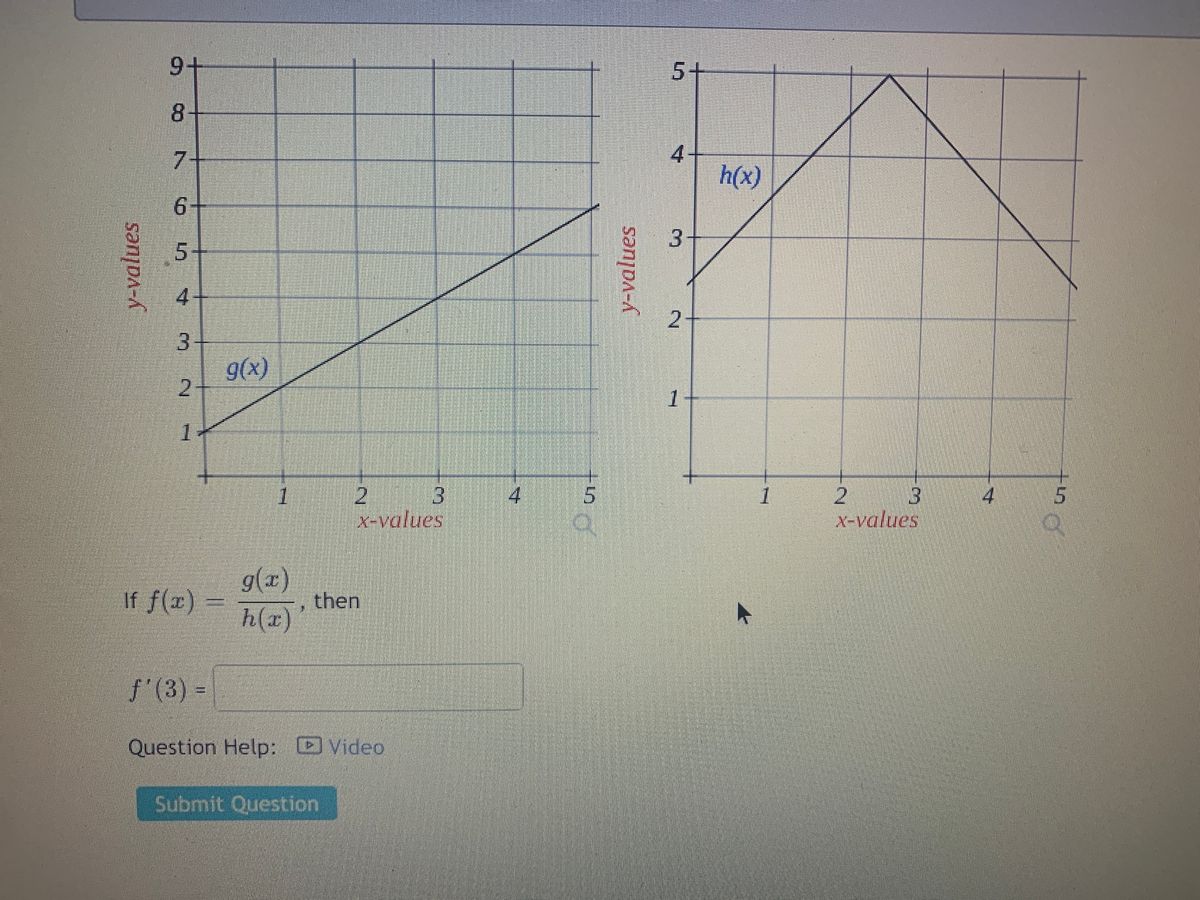



Answered 9 5 8 7 H X 6 4 3 9 X 1 1 2 3 Bartleby



Solved If F X X2 2 And G X X 3 Then Findfog H Select One H3 3 H2 2h 6 B H2 5 C H2 11 D Course Hero
Eq1) or equivalently if the following equation holds for all such x f (x) − f (− x) = 0 {\displaystyle f(x)f(x)=0} Geometrically, the graph of an even function is symmetric with respect to the y axis, meaning that its graph remains unchanged after reflection about the y axis Examples of even functions are The absolute value x ↦ x , {\displaystyle x\mapsto x,} x ↦ x 2Extended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, musicAnd so on Here are useful rules to help you work out the derivatives of many functions (with examples below)Note the little mark ' means derivative of, and



Horizontal Stretch Properties Graph Examples




If G X Frac 12 Frac 19 X 2 4 2 Is Obtained By Doing G X F Kx Horizontal Stretch Of Function F What Is Number K Mathematics Stack Exchange
F(x) = 1/x, g(x) = 1/xExamples Below is the graph of f R !By signing up, you'll get thousands of stepbystep solutions to your homework




Answered 1 7 2 6 H 4 X 12 6 G X 3 F X 9 3 1 Bartleby



Algebra 1 State Test Practice Algebra House
R where f(x)=x2 Using techniques learned in the chapter "Intro to Graphs", we can see that the range of f is 0,1) The target of f is R,and0,1) 6= R so f is not onto Below is the graph of g R !I will plug the formula for g(x) into every instance of "x" in the formula for f (x) Now I will plug the formula for f (x) into every instance of "x" in the formula for g(x) Both ways, I ended up with just "x", so f (x) and g(x) are inverses of each otherDetermine algebraically whether f (x) = 3x – 2 and g(x) = (1 / 3)x 2 are inverses of each other 1 Answer AJ Speller (f ∘ g)(x) = f (g(x)) = f (x 2) = (x 2)2 Click on the link below to see another example



Brazosport Edu Assets Faculty Agut Calin 2413 Review 2 calculus i Pdf




اسئلة محلولة عن الدوال والنهايات
g(x)= x^(3 ) 3x^212 We have to find (fg)(x)= ?Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more f(x)=19x2→ Switch the f(x) with a y y=19x2→ Switch the places of the x and the y variables x=19y2→ Solve for y x−2=19y y=9x−18 The inverse is f−1(x)=9x−18




Writing Exponential Functions From Graphs Algebra Video Khan Academy



Http Www Cusd80 Com Cms Lib6 Az Centricity Domain 2148 Q1 exam review 13 14 key pdf Pdf
F (g (2)), g (x)=2x1, f (x)=x^2 \square!F(x)=x4−9 g(x)=x39 (f⋅g)(x)= Thanks so much!Find the Properties f (x)=x^28x9 f (x) = x2 − 8x − 9 f ( x) = x 2 8 x 9 Rewrite the equation in vertex form Tap for more steps Complete the square for x 2 − 8 x − 9 x 2 8 x 9 Tap for more steps Use the form a x 2 b x c a x 2 b x c, to find the values of a a, b b, and c c a = 1, b = − 8, c = − 9 a = 1, b



Http Www Mpsaz Org Rmhs Staff Esritter Collegealgebra Files 8 1 Handout Key Pdf



2
The operations on functions are as easy as the operations on numbers or polynomials We have to subtract the functions to find the above mentioned operation =(fg)(x)=f(x)g(x) (fg)(x)=x^4 x^29x^(3 ) 3x^212 The minus will change the signs of function g = x^4 x^29 x^(3 ) 3x^212If f(x) = 3x 9 and g(x) = x^2, what is (g บ f)(5)?gf(x) = g3x9 = (3x9)^2 = 9x^2 54x 81Cheers,It is given g(x1)=x^21 Put x1 at the place of x, g{(x1)1}=(x1)^21 => g(x11)=x^22x11^21 {since (ab)^2= a^22abb^2} => g(x)=x^22x11 => g(x)=x^22x2
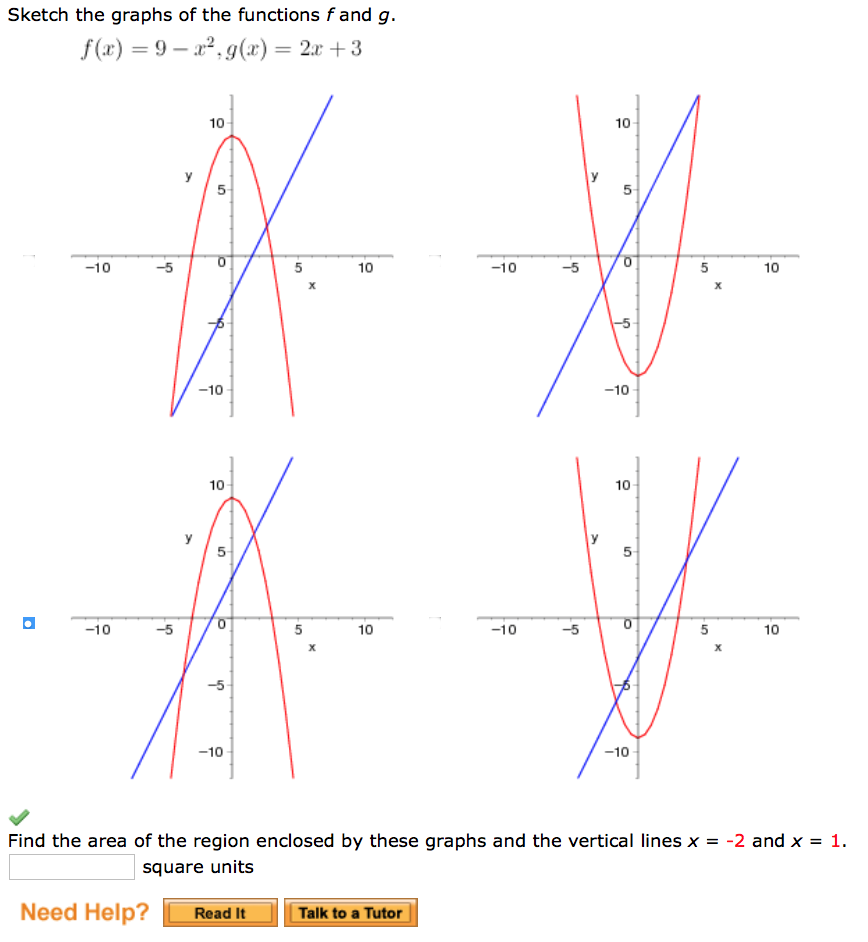



Sketch The Graphs Of The Functions F And G F X 9 Chegg Com




Use The Graph Of F X And G X To Evaluate F G 1 Mathematics Stack Exchange
f(x) = (2 x^(1/2)) and g(x) = x^2 9 so, g(x) f(x) = (x^2 9)/(2 x^(1/2)) Now, the denominator cannot be zero ie 2 x^(1/2)!= 0 so, x^(1/2)!= 2 Hence, x!= 4 Therefore, the domain is all values except x = 4 )>Answer is g f (x) = 3 2 x 1 x Explanation f (x) = 1 x g (x) = x 2 1 3 x 2 Let f(x) = \\frac{x^2}{x^2 1}find the largest integer n so that f(2) \\cdot f(3) \\cdot f(4) \\cdots f(n1) \\cdot f(n) < 1



Suppose F X X 2 What Is The Graph Of G X 1 2f X




What Are The Local Extrema Of F X X 3 X 2 5x 4 X 2 2 Socratic



Schoolwires Henry K12 Ga Us Cms Lib08 Ga Centricity Domain 6309 228 Composite functions review Key Pdf



Evaluate The Function G X 2x2 3x 5 For The Input Values 2




F X X 2 What Is G X Brainly Com




If F X F X Is A Differentiable Function And G X G X Is A Double Differentiable Function Such That F X 1 F X 1 And F 39 X G X F X G X If F2 0 G2 0 9f2 Vf5dz0tt Mathematics Topperlearning Com



Http Www Nicolet K12 Wi Us Faculty Dgibbon Day 22 answer key Pdf



Faculty Millikin Edu Pstickles Derivatives With Table Practice Answers Pdf




Answered F X 2x 1 And G X X 9 2 A F O Bartleby



F X X 3



Www Claytonschools Net Cms Lib Mo Centricity Domain 4 2 ap prob soln Pdf




F X X 2 What Is G X Brainly Com




Let Gx T Dt Where F Is The Function Whose Graph Is Shown A Evaluate Gtx For X 0 1 2 3 4 5 And 6 Gt1 1 2 0t2 0 G 3 1 2 Ot4 0 9 5 3 2 9 6 4 B Estimate G 7 Use The Midpo Homeworklib




Quantitative Aptitude Algebra Functions If F X 5x 2 3x 5 Handa Ka Funda Online Coaching For Cat And Banking Exams



Suppose F X X 2 What Is The Graph Of G X F 2x



F X X 2 What Is G X 1 4




Static Doubtnut Com Q Thumbnail Png



What Is F X And G X If F 2x 1 G X 1 X And F 2x 1 2g X 1 2x 2 Is Satisfied Quora



Www Scarsdaleschools K12 Ny Us Cms Lib Ny Centricity Domain 222 Function worksheets on composition from elise with answer key hw Pdf



Www Mochidoesmaths Com Composition of functions i Pdf



Graph Exponential Functions Using Transformations College Algebra




Rd Sharma Solutions For Class 12 Chapter 2 Functions




Ex 2 Graph Two Translations Of The Basic Rational Function F X 1 X Youtube



2




Additional Mathematics Functions Questions 1 Given Function F X Mx 4 X N X N If F 2 10 And F 8 4 Find A The Values Of M And N B The Ppt Download



Http Www Hanbommoon Net Wp Content Uploads 13 08 Homework 9 Model Solution Pdf



Sites Levittownschools Com Cbergersen Documents Unit 2 hw answers Pdf




Given F 2 X G 2 X H 2 X 9 And U X 3f X 4g X 10h X Where F X G X And H X Are Continuous X R If Maximum Value Of U X Is



Http Winwoodmaths Online Wp Content Uploads 19 05 Functions Ibsl Ans Pdf
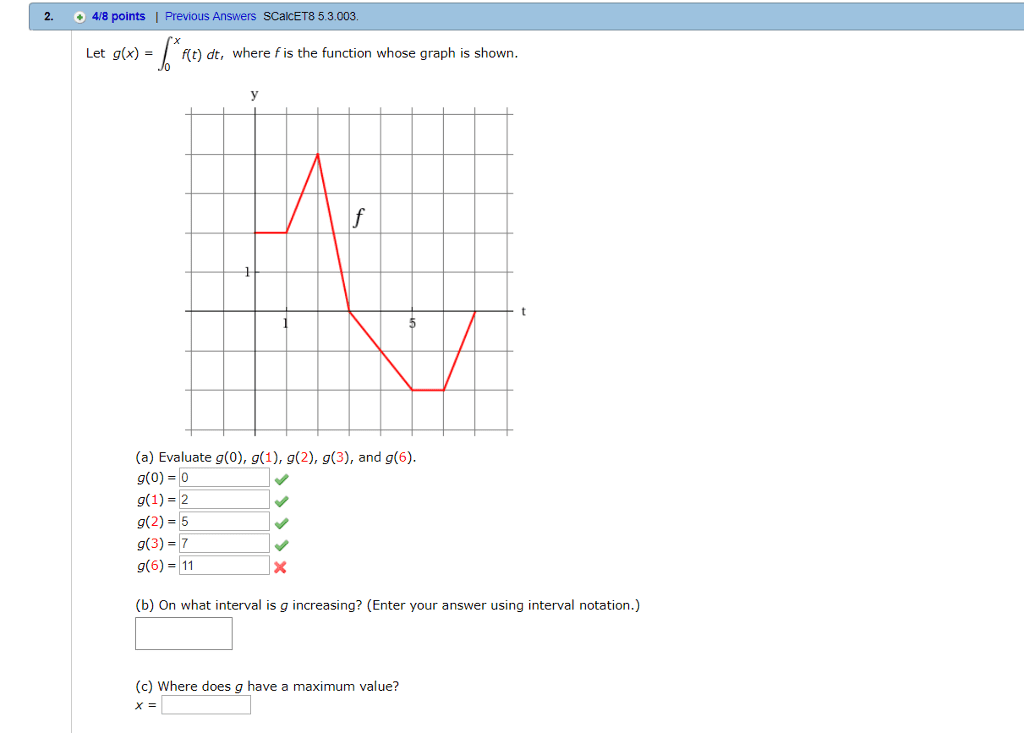



Oneclass 2 4 8 Points Previous Answers Scalcet8 5 3 003 Let G X F T Dt Where Fis The Function W




G X 2 1 2 X 1 3 Verify Transformation Of Key Points Between Functions Youtube



View Question What Is F G X



Www Cbsd Org Cms Lib Pa Centricity Domain 2780 1 9 inverse functions presentation pdf Pdf



Www Humbleisd Net Cms Lib2 Tx Centricity Domain 3611 Answer review final exam fall Pdf



Efisd Net Common Pages Displayfile Aspx Itemid



Grade 12 Paper 1 The Graphs Of F X Frac 1 2 X 5 2 8 And G X Frac 1 2 X Frac 9 2 Are Sketched Below Mathsgee Answer Hub




Basic Derivative Rules Table Video Khan Academy



Http Www Scasd Org Cms Lib5 Pa Centricity Domain 12 Key graded wksh 76 77 Pdf



Math Scene Equations Iii Lesson 3 Quadratic Equations



Http Www Lcps Org Cms Lib4 Va Centricity Domain 3768 Afm unit 4 day 1 Pdf



How Do You Find The Area Between F X X 2 2x 1 G X 3x 3 Socratic




Solved If G X 4 X 2 X 9 Find G 2 G 1 And G 3 2 7924



2



Www Scasd Org Cms Lib Pa Centricity Domain 1229 Unit 5 note packet mplg Pdf




F X And G X Are Two Differentiable Function In 0 2 Such That F X G X 0 F 1 2 G 1 4 F 2 3 G 2 9 Then F X G X Atx 3 2 Is
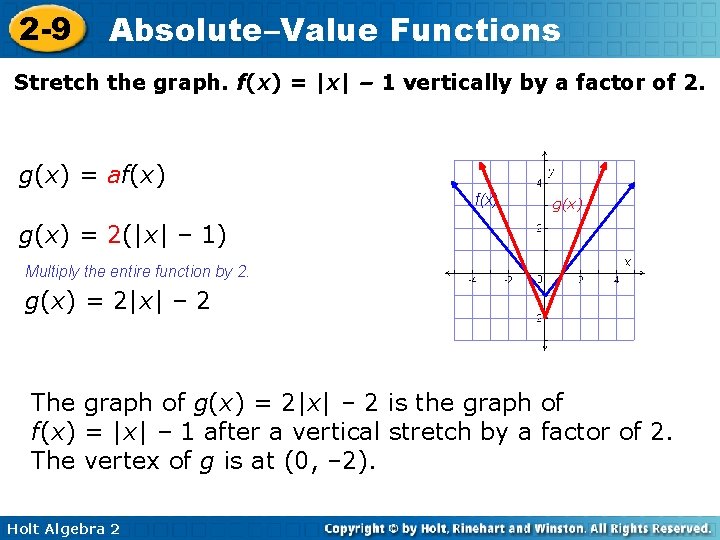



2 9 Absolutevalue Functions Objective Graph And Transform




Given That Lim F X 9 Lim G X 2 Lim H X 0 X Chegg Com



If The Function F R To R Be Given By F X X 2 And G R To R Be Given By G X X X 1 X Not Equal To 1 Find Fog




Additional Mathematics Functions Questions 1 Given Function F X Mx 4 X N X N If F 2 10 And F 8 4 Find A The Values Of M And N B The Ppt Download




Find The Area Of The Region Enclosed Between 𝑓 𝑥 0 5𝑥2 7 F X 0 5 X 2 7 𝑔 𝑥 𝑥 G X X 𝑥 5 X



Solved Given That F X 2x 3 And G X 9x 2 5x 11 Determine The Following Course Hero



Http Www Webassign Net Latex2pdf 516dc973ddcbd6bc42f3 Pdf




Are Inverses F X




Solution Manual Chapter 07 Exponential Logarithmic And Inverse T



Http Blogs Waukeeschools Org Csitzmann Files 14 11 Chapter 6 Worksheet Answers 2 Pdf




Chapter 2 Problems



Http Www Basd K12 Wi Us Faculty Mbuteyn Chapter 6 review key Pdf
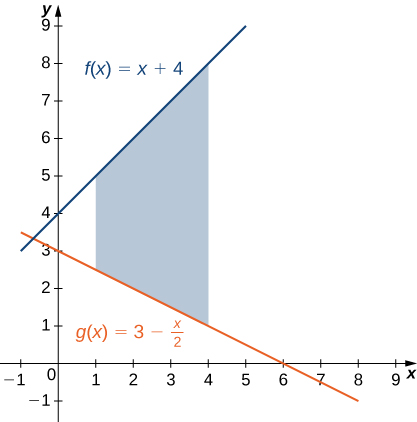



6 1 Areas Between Curves Calculus Volume 1



Http Cbsd Org Cms Lib010 Pa Centricity Domain 49 Day 8 section 1 9 inverse functions f16 class notes Pdf



Http Mail Csufresno Edu Mnogin Math75spring04 75review11 33sol Pdf



Secure Media Collegeboard Org Digitalservices Pdf Ap Ap17 Calculus Ab Q6 Pdf



Sites Levittownschools Com Cbergersen Documents Unit 2 hw answers Pdf



Http Mail Csufresno Edu Mnogin Math75summer05 75review11 34prob Pdf




If F X X 2 2 And G X 4f X 1 Then Which Of The Following Is The Value Of G 3 Wyzant Ask An Expert



Www Freeport K12 Pa Us Userfiles 8 Classes 54 Free response day 2 solutions Pdf Id 5597



Www Livingston Org Cms Lib4 Nj Centricity Domain 1242 Function operation kuta practiice answer key Pdf
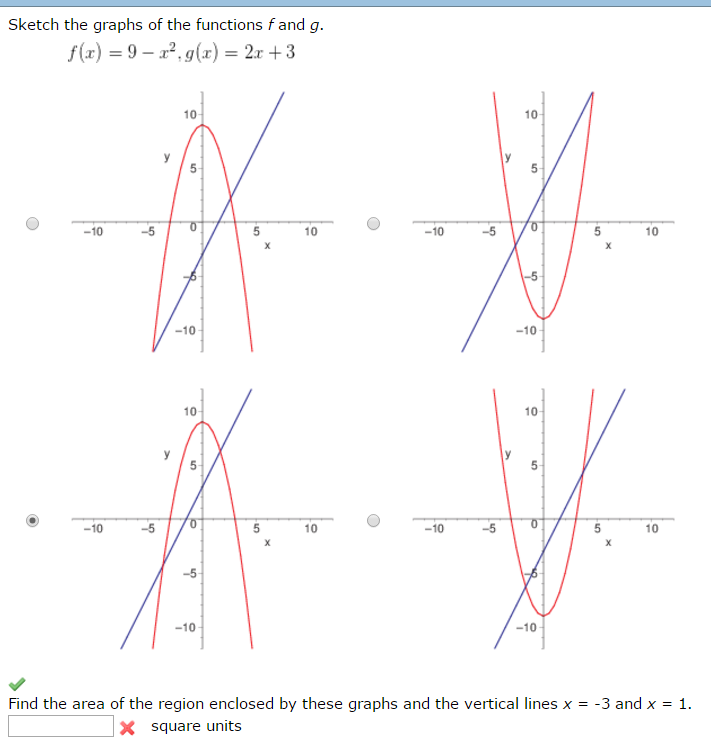



Sketch The Graphs Of The Functions F And G F X Chegg Com




Consider The Following F X X 4 9x 2 G X X 2 9 A Graph The Region Bounded By The Graphs Of The Equations B Find The Area Of The Region Analytically


